
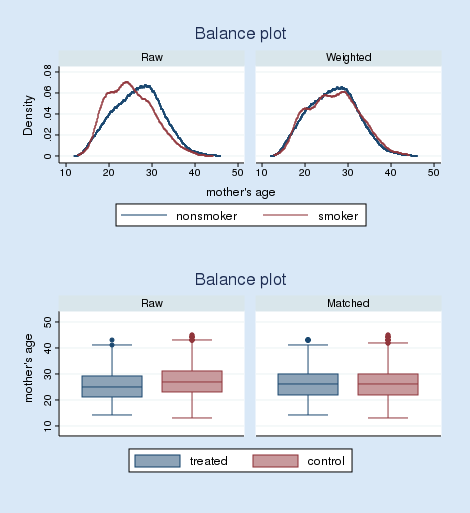
We might ask, “How would the outcomes have changed had the mothers who smoked chosen not to smoke?” or “How would the outcomes have changed had the mothers who didn’t smoke chosen to smoke?”. RA estimators model the outcome to account for the nonrandom treatment assignment. Thus, mother’s age is related to both treatment status and outcome. In these data, older mothers were also more likely to be smokers. Older mothers tend to have heavier babies regardless of whether they smoked while pregnant. We cannot estimate the effect of smoking on birthweight by comparing the mean birthweights of babies of mothers who did and did not smoke. The mothers themselves chose whether to smoke, and that complicates the analysis. The red points represent the mothers who smoked during pregnancy, while the green points represent the mothers who did not. The treatment variable is the mother’s smoking status during pregnancy, and the outcome is the birthweight of her baby. Figure 1 is a scatterplot of observational data similar to those used by Cattaneo (2010). If our model is correct, the treatment assignment process is considered as good as random conditional on the covariates in our model. For observational data, we model the treatment assignment process.
For experimental data, random assignment of the treatment guarantees that the treatment is independent of the outcome so averages of the outcomes conditional on observed treatment estimate the unconditional means of interest. We only observe the outcome of each subject conditional on the received treatment regardless of whether the data are observational or experimental. Randomly assigning the treatment guarantees that the treatment is independent of the outcome, which greatly simplifies the analysis.Ĭausal inference requires the estimation of the unconditional means of the outcomes for each treatment level. We would randomly assign subjects to the treated or untreated groups. In an ideal world, we would design an experiment to test cause-and-effect and treatment-and-outcome relationships. The subjects are said to have self-selected into the treated and untreated groups. For example, a mother decides to smoke or not to smoke. The problem with observational data is that the subjects choose whether to get the treatment. Questions like this one can only be answered using observational data. A treatment could even be an ad campaign designed to increase the sales of a product.Ĭonsider whether a mother’s smoking affects the weight of her baby at birth. A treatment could be a job training program and the outcome employment or wages. A treatment could be a surgical procedure and the outcome patient mobility. We are going to discuss treatments and outcomes.Ī treatment could be a new drug and the outcome blood pressure or cholesterol levels. As with any regression analysis of observational data, the causal interpretation must be based on a reasonable underlying scientific rationale. We should note that nothing about treatment-effects estimators magically extracts causal relationships. We’ll save the matching estimators for part 2.



 0 kommentar(er)
0 kommentar(er)
